
Although both Berenger's formulation and UPML were initially derived by manually constructing the conditions under which incident plane waves do not reflect from the PML interface from a homogeneous medium, both formulations were later shown to be equivalent to a much more elegant and general approach: stretched-coordinate PML.

A later formulation that has become more popular because of its simplicity and efficiency is called uniaxial PML or UPML, in which the PML is described as an artificial anisotropic absorbing material. Berenger's original formulation is called a split-field PML, because it splits the electromagnetic fields into two unphysical fields in the PML region.
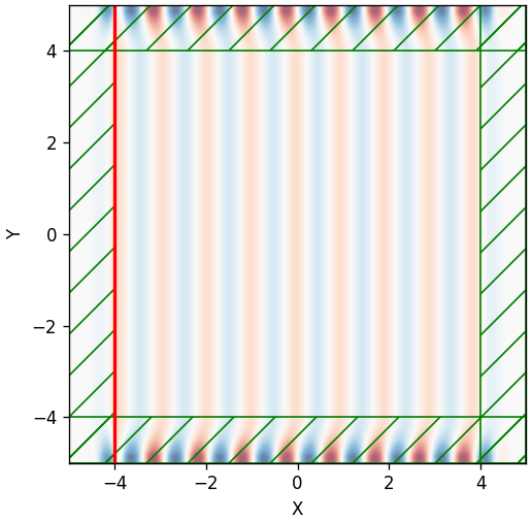
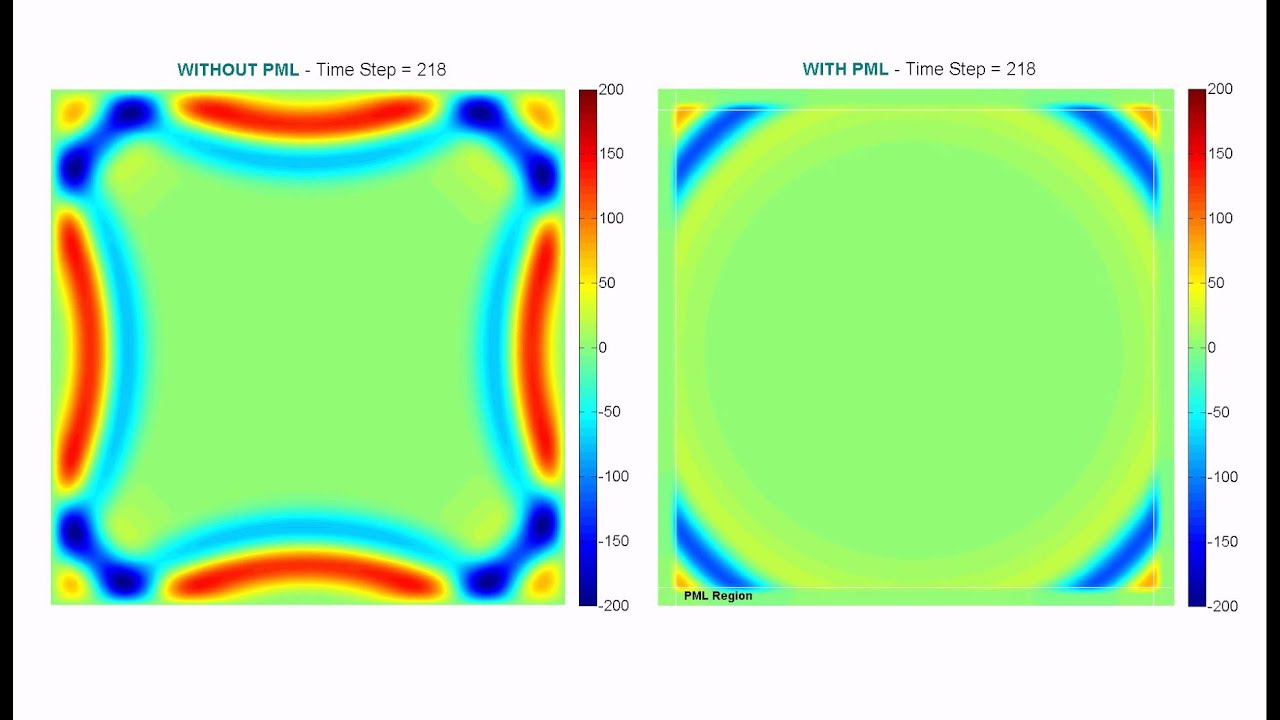
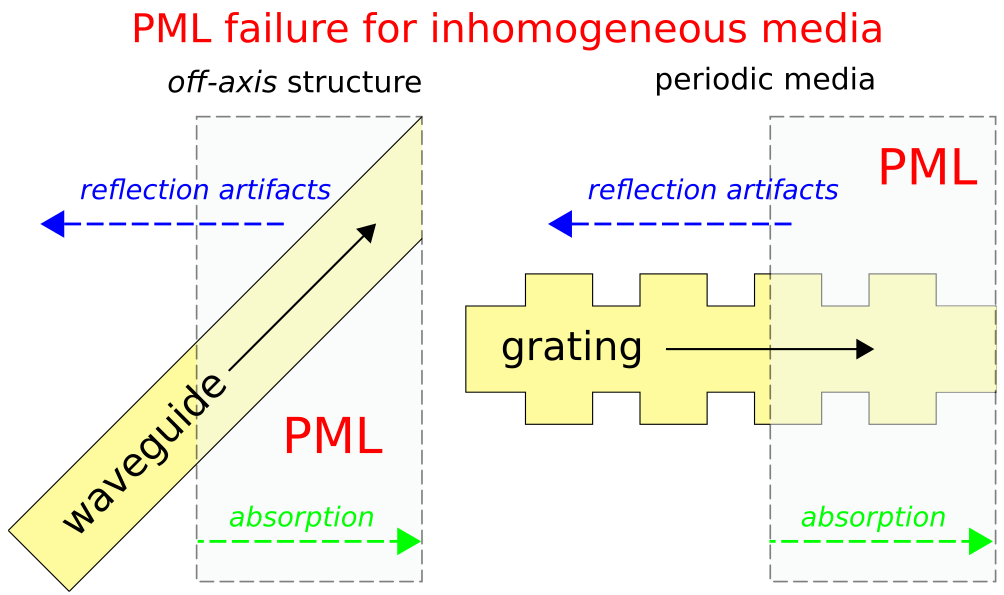
PML was originally formulated by Berenger in 1994 for use with Maxwell's equations, and since that time there have been several related reformulations of PML for both Maxwell's equations and for other wave-type equations, such as elastodynamics, the linearized Euler equations, Helmholtz equations, and poroelasticity. The key property of a PML that distinguishes it from an ordinary absorbing material is that it is designed so that waves incident upon the PML from a non-PML medium do not reflect at the interface-this property allows the PML to strongly absorb outgoing waves from the interior of a computational region without reflecting them back into the interior. The striped borders correspond to perfectly matched layers, which are used to simulate open boundaries by absorbing the outgoing waves.Ī perfectly matched layer ( PML) is an artificial absorbing layer for wave equations, commonly used to truncate computational regions in numerical methods to simulate problems with open boundaries, especially in the FDTD and FE methods. A FDTD scheme for a light scattering problem.


 0 kommentar(er)
0 kommentar(er)
